应用场景
在互联网后台的开发工作中,笔者会经常遇到各种各样的**白名单**业务场景,比如以下典型场景:
- 现有1亿个用户
user_id,如何快速判断一个user_id是否在该白名单内 - 网络爬虫解析出一个页面的
url清单,如何快速判断该url是否已经被抓取过 - 现有1亿个
user_id,如何快速判断哪些user_id曾重复出现 - 服务器收到来自某个
ip地址的请求,快速判断该ip地址是否在黑名单 - ……
熟悉数据结构的读者,略微思考一下,便知以上若干问题的核心需求是:*设计一个内存占用少且又高效的查找算法/数据结构。*** 以场景1为例,大多数读者首先想到的数据结构为*哈希表***,任意元素均可在O(1)时间复杂度内快速完成查找。
假设哈希表的装载因子为0.5(实践中比较常见的取值),粗略计算一下1亿个int类型user_id的内存占用约为745MB,一个白名单要占用如此多的内存空间,这显然是不可接受的。那么我们如何既能达成我们的目的,又占用比较小的内存呢?
一个user_id是否在白名单之内,只可能存在两种取值——是/否,从**香农信息论** 角度来看,使用1个bit即可表示是/否两种取值。一个int类型变量可存储2^32种取值,而当前业务场景下我们仅仅需要0和1两种状态便可(存储4种状态使用2个bit,存储8种状态使用3个bit,以此类推…)。存储1亿个bit占用空间约为11MB,大大减少了内存占用,这便是Bitmap数据结构。
Bitmap
Bitmap是一种紧凑的数据结构。以场景1为例,首先在内存中连续分配1亿个bit,要判断user_id为1000的用户是否在白名单之内,只需获取bit序列的第1000位bit的状态(1:user_id在白名单,0:user_id不在白名单)。如下为c语言版本的示例代码(也可查看笔者的github):
1 |
|
Bitmap类似于哈希表,哈希规则便是将数字n映射到Bitmap第n个bit上。因此Bitmap在实际应用中存在一处问题——当n取值特别大时,Bitmap占用空间也会比较大。在此业务场景下,Bitmap数据结构是不合理的,所以便衍生出了Bloom Filter。
Bloom Filter
Bloom Filter,中文译名布隆过滤器,是1970年由布隆提出来。布隆过滤器可以用于检索一个元素是否在一个集合中。朴素的讲,BloomFilter在Bitmap的基础上,将Hash函数的由一个扩展至多个。判断一个元素是否在一个集合中,仅需判断经过这些Hash函数后的值是否置位。布隆过滤器优点是*空间复杂度和时间复杂度*** 都优于一般的算法,缺点是*有一定的误识别率*** ,删除困难。
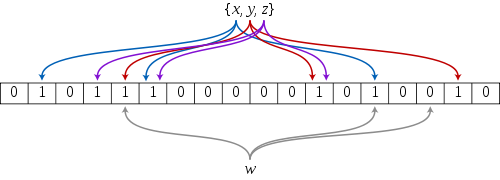
算法原理
假设所选Hash函数在散列空间内分布均匀,即散列到每一个位置的概率相等(对于Hash函数的核心诉求)。假设Bit数组的大小为m,k为Hash函数的个数。
Bit数组中某一位位置在元素插入时的Hash操作中没有被置位1的概率是:
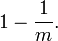
k个Hash函数散列之后该位置仍未被置位1的概率是:
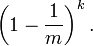
连续插入n个元素,该位置仍未被置位1的概率是:
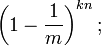
对立事件,该位为1的概率为:
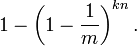
代码实现
C语言实现请参考笔者Github:bloomfilter.c

